Công thức tính chu vi và diện tích tam giác [đầy đủ các loại tam giác]
Sau đây Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giới thiệu đến quý thầy cô và các bạn học sinh đầy đủ các công thức tính chu vi và diện tích tam giác gồm: tam giác thường, tam giác đều, tam giác cân, tam giác vuông, tam giác vuông cân. Nếu mọi người muốn tìm hiểu sâu hơn các kiến thức về tam giác, hãy chia sẻ ngay bài viết sau đây nhé !
I. Tam giác là gì ? Có mấy loại tam giác ?
1. Định nghĩa:
Tam giác là hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Một tam giác có các cạnh AB, BC và AC được ký hiệu là 
2. Phân loại tam giác:
Tam giác có 4 loại tam giác đặc biệt :

– Tam giác cân: là tam giác có hai cạnh bằng nhau.
– Tam giác đều: là tam giác có ba cạnh bằng nhau.
– Tam giác vuông: là tam giác có một góc vuông.
– Tam giác vuông cân: là tam giác vuông có hai cạnh góc vuông bằng nhau.
3. Một số tính chất của tam giác
- Tổng các góc trong của một tam giác bằng 180° (định lý tổng ba góc trong của một tam giác).
- Độ dài mỗi cạnh lớn hơn hiệu độ dài hai cạnh kia và nhỏ hơn tổng độ dài của chúng (bất đẳng thức tam giác).
- Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. Ngược lại, góc đối diện với cạnh lớn hơn là góc lớn hơn (quan hệ giữa cạnh và góc đối diện trong tam giác).
- Ba đường cao của tam giác cắt nhau tại một điểm được gọi là trực tâm của tam giác (đồng quy tam giác).
- Ba đường trung tuyến của tam giác cắt nhau tại một điểm được gọi là trọng tâm của tam giác. Khoảng cách từ trọng tâm đến cạnh của tam giác bằng 2/3 độ dài các đường trung tuyến. Đường trung tuyến của tam giác chia tam giác thành hai phần có diện tích bằng nhau (đồng quy tam giác).
- Ba đường trung trực của tam giác cắt nhau tại một điểm là tâm đường tròn ngoại tiếp của tam giác (đồng quy tam giác).
- Ba đường phân giác trong của tam giác cắt nhau tại một điểm là tâm đường tròn nội tiếp của tam giác (đồng quy tam giác).
II. Công thức tính chu vi tam giác
1. Công thức tính chu vi tam giác thường
Tam giác thường là loại tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.
– Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó.
– Công thức: P = a + b + c
Trong đó:
- P là chu vi tam giác
- a, b, c lần lượt là độ dài 3 cạnh của tam giác.
2. Công thức tính chu vi tam giác cân
Tam giác cân là tam giác có 2 cạnh, 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.
– Chu vi tam giác cân bằng 2 lần cạnh bên cộng với cạnh đáy.
– Công thức: P = 2.a + c
Trong đó:
- a là độ dài hai cạnh bên của tam giác cân,
- c là độ dài cạnh đáy của tam giác.
3. Công thức tính chu vi tam giác đều
Tam giác đều là tam giác có 3 cạnh, 3 góc nhọn bằng nhau, là trường hợp đặc biệt của tam giác cân.
– Chu vi tam giác đều bằng tổng độ dài ba cạnh, mà ba cạnh của tam giác bằng nhau nên tức bằng độ dài một cạnh nhân ba.
– Công thức: P = a + a + a = 3 x a
Trong đó:
- P là chu vi tam giác đều
- a là độ dài cạnh của tam giác
4. Công thức tính chu vi tam giác vuông
Tam giác vuông là tam giác có 1 góc bằng 90°.
– Chu vi hình tam giác vuông bằng tổng chiều dài 3 cạnh của tam giác.
– Công thức: P = a + b + c
Trong đó:
- a và b là độ dài hai cạnh của tam giác vuông
- c là độ dài cạnh huyền của tam giác vuông.
III. Công thức tính diện tích tam giác
1. Công thức tính diện tích tam giác thường

Công thức thông dụng nhất: Muốn tính diện tích tam giác ta lấy độ dài cạnh đáy nhân đường cao rồi chia 2 ( hay Diện tích tam giác được xác định bằng một phần hai của cạnh đáy nhân với chiều cao tương ứng)
S = 1/2a.h = 1/2 b.h = 1/2 c.h
Ngoài ra, ở các chương trình học cao hơn, các bạn có thể sử dụng hệ thức hê rông để tính diện tích của tam giác, khi biết độ dài ba cạnh.
Ví dụ , a, b,c lần lượt là độ dài 3 cạnh của 1 tam giác.
Khi đó ta có nửa chu vi tam giác là
P=a+b+c/2
Áp dụng hệ thức Hê- rông, diện tích tam giác sẽ được tính như sau
– Công thức heron:

Hệ thức Hê-rông được áp dụng bắt đầu từ bậc phổ thông, và có tính ứng dụng khá cao để giải các bài toán hình học phức tạp.
Ngoài hai công thức trên, bạn cũng có thể áp dụng công thức tính diện tích của tam giác bằng sin như sau:
Ba cạnh của một tam giác lần lượt là a,b,c, các góc được tạo bởi các cạnh lần lượt là A,B,C. Khi đó ta có thể tính diện tích của tam giác như sau:

2. Công thức tính diện tích tam giác vuông

Tam giác vuông là một trong những trường hợp đặc biệt, có hai cạnh tạo với nhau một góc 90 độ, gọi là hai cạnh góc vuông
Ví dụ, có tam giác vuông có hai cạnh góc vuông lần lượt là a và b
Khi đó, công thức tính diện tích của tam giác sẽ là:
S= ab/2
3. Công thức tính diện tích tam giác đều

Công thức tính diện tích của tam giác đều cũng dựa trên nguyên lý của công thức tính diện tích của tam giác tam giác thường. Tuy nhiên do đây là trường hợp đặc biệt có chiều cao trùng với đường trung tuyến, nên ta có thể áp dụng công thức tính nhanh khi biết cạnh của tam giác.
Ví dụ, có tam giác đều, cạnh bằng a
Khi đó ta có công thức tính diện tích tam giác như sau:
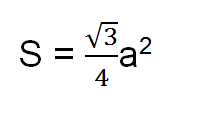
4. Công thức tính diện tích tam giác cân

– Diện tích tam giác cân bằng tích chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, rồi chia cho 2.
– Công thức:
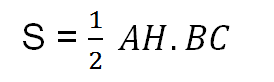
Trong đó:
- BC là độ dài cạnh đáy
- AH là chiều cao từ đỉnh A tới cạnh đáy BC.
Vậy là chúng tôi đã giới thiệu đến bạn các công thức tính chu vi tam giác, tính diện tích tam giác với đầy đủ các loại tam giác. Hi vọng, sau khi chia sẻ cùng bài viết, các bạn đã có thêm nhiều kiến thức bổ ích. Bên cạnh đó, các công thức tính chu vi và diện tích hình vuông cũng đã được Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội books giới thiệu rất chi tiết. Bạn đừng bỏ lỡ nhé !
Công thức tính chu vi và diện tích tam giác [đầy đủ các loại tam giác]
Sau đây Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội sẽ giới thiệu đến quý thầy cô và các bạn học sinh đầy đủ các công thức tính chu vi và diện tích tam giác gồm: tam giác thường, tam giác đều, tam giác cân, tam giác vuông, tam giác vuông cân. Nếu mọi người muốn tìm hiểu sâu hơn các kiến thức về tam giác, hãy chia sẻ ngay bài viết sau đây nhé !
I. Tam giác là gì ? Có mấy loại tam giác ?
1. Định nghĩa:
Tam giác là hình hai chiều phẳng có ba đỉnh là ba điểm không thẳng hàng và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là đa giác có số cạnh ít nhất (3 cạnh). Một tam giác có các cạnh AB, BC và AC được ký hiệu là 
2. Phân loại tam giác:
Tam giác có 4 loại tam giác đặc biệt :

– Tam giác cân: là tam giác có hai cạnh bằng nhau.
– Tam giác đều: là tam giác có ba cạnh bằng nhau.
– Tam giác vuông: là tam giác có một góc vuông.
– Tam giác vuông cân: là tam giác vuông có hai cạnh góc vuông bằng nhau.
3. Một số tính chất của tam giác
- Tổng các góc trong của một tam giác bằng 180° (định lý tổng ba góc trong của một tam giác).
- Độ dài mỗi cạnh lớn hơn hiệu độ dài hai cạnh kia và nhỏ hơn tổng độ dài của chúng (bất đẳng thức tam giác).
- Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn. Ngược lại, góc đối diện với cạnh lớn hơn là góc lớn hơn (quan hệ giữa cạnh và góc đối diện trong tam giác).
- Ba đường cao của tam giác cắt nhau tại một điểm được gọi là trực tâm của tam giác (đồng quy tam giác).
- Ba đường trung tuyến của tam giác cắt nhau tại một điểm được gọi là trọng tâm của tam giác. Khoảng cách từ trọng tâm đến cạnh của tam giác bằng 2/3 độ dài các đường trung tuyến. Đường trung tuyến của tam giác chia tam giác thành hai phần có diện tích bằng nhau (đồng quy tam giác).
- Ba đường trung trực của tam giác cắt nhau tại một điểm là tâm đường tròn ngoại tiếp của tam giác (đồng quy tam giác).
- Ba đường phân giác trong của tam giác cắt nhau tại một điểm là tâm đường tròn nội tiếp của tam giác (đồng quy tam giác).
II. Công thức tính chu vi tam giác
1. Công thức tính chu vi tam giác thường
Tam giác thường là loại tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.
– Chu vi tam giác bằng độ dài tổng ba cạnh của tam giác đó.
– Công thức: P = a + b + c
Trong đó:
- P là chu vi tam giác
- a, b, c lần lượt là độ dài 3 cạnh của tam giác.
2. Công thức tính chu vi tam giác cân
Tam giác cân là tam giác có 2 cạnh, 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.
– Chu vi tam giác cân bằng 2 lần cạnh bên cộng với cạnh đáy.
– Công thức: P = 2.a + c
Trong đó:
- a là độ dài hai cạnh bên của tam giác cân,
- c là độ dài cạnh đáy của tam giác.
3. Công thức tính chu vi tam giác đều
Tam giác đều là tam giác có 3 cạnh, 3 góc nhọn bằng nhau, là trường hợp đặc biệt của tam giác cân.
– Chu vi tam giác đều bằng tổng độ dài ba cạnh, mà ba cạnh của tam giác bằng nhau nên tức bằng độ dài một cạnh nhân ba.
– Công thức: P = a + a + a = 3 x a
Trong đó:
- P là chu vi tam giác đều
- a là độ dài cạnh của tam giác
4. Công thức tính chu vi tam giác vuông
Tam giác vuông là tam giác có 1 góc bằng 90°.
– Chu vi hình tam giác vuông bằng tổng chiều dài 3 cạnh của tam giác.
– Công thức: P = a + b + c
Trong đó:
- a và b là độ dài hai cạnh của tam giác vuông
- c là độ dài cạnh huyền của tam giác vuông.
III. Công thức tính diện tích tam giác
1. Công thức tính diện tích tam giác thường

Công thức thông dụng nhất: Muốn tính diện tích tam giác ta lấy độ dài cạnh đáy nhân đường cao rồi chia 2 ( hay Diện tích tam giác được xác định bằng một phần hai của cạnh đáy nhân với chiều cao tương ứng)
S = 1/2a.h = 1/2 b.h = 1/2 c.h
Ngoài ra, ở các chương trình học cao hơn, các bạn có thể sử dụng hệ thức hê rông để tính diện tích của tam giác, khi biết độ dài ba cạnh.
Ví dụ , a, b,c lần lượt là độ dài 3 cạnh của 1 tam giác.
Khi đó ta có nửa chu vi tam giác là
P=a+b+c/2
Áp dụng hệ thức Hê- rông, diện tích tam giác sẽ được tính như sau
– Công thức heron:

Hệ thức Hê-rông được áp dụng bắt đầu từ bậc phổ thông, và có tính ứng dụng khá cao để giải các bài toán hình học phức tạp.
Ngoài hai công thức trên, bạn cũng có thể áp dụng công thức tính diện tích của tam giác bằng sin như sau:
Ba cạnh của một tam giác lần lượt là a,b,c, các góc được tạo bởi các cạnh lần lượt là A,B,C. Khi đó ta có thể tính diện tích của tam giác như sau:

2. Công thức tính diện tích tam giác vuông

Tam giác vuông là một trong những trường hợp đặc biệt, có hai cạnh tạo với nhau một góc 90 độ, gọi là hai cạnh góc vuông
Ví dụ, có tam giác vuông có hai cạnh góc vuông lần lượt là a và b
Khi đó, công thức tính diện tích của tam giác sẽ là:
S= ab/2
3. Công thức tính diện tích tam giác đều

Công thức tính diện tích của tam giác đều cũng dựa trên nguyên lý của công thức tính diện tích của tam giác tam giác thường. Tuy nhiên do đây là trường hợp đặc biệt có chiều cao trùng với đường trung tuyến, nên ta có thể áp dụng công thức tính nhanh khi biết cạnh của tam giác.
Ví dụ, có tam giác đều, cạnh bằng a
Khi đó ta có công thức tính diện tích tam giác như sau:
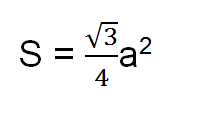
4. Công thức tính diện tích tam giác cân

– Diện tích tam giác cân bằng tích chiều cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, rồi chia cho 2.
– Công thức:
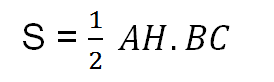
Trong đó:
- BC là độ dài cạnh đáy
- AH là chiều cao từ đỉnh A tới cạnh đáy BC.
Vậy là chúng tôi đã giới thiệu đến bạn các công thức tính chu vi tam giác, tính diện tích tam giác với đầy đủ các loại tam giác. Hi vọng, sau khi chia sẻ cùng bài viết, các bạn đã có thêm nhiều kiến thức bổ ích. Bên cạnh đó, các công thức tính chu vi và diện tích hình vuông cũng đã được Trường TCSP Mẫu giáo – Nhà trẻ Hà Nội books giới thiệu rất chi tiết. Bạn đừng bỏ lỡ nhé !

